Μια κάποια κλιματική ευαισθησία

Ο Svante Arrhenius γύρω στο 1910

Ο Σουηδός φυσικοχημικός Svante August Arrhenius ήταν ο πρώτος που υπολόγισε την σχέση της μέσης θερμοκρασίας του πλανήτη με την συγκέντρωση του διοξειδίου του άνθρακα στην ατμόσφαιρα, στην εργασία του με τίτλο 'On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground'. Στα συμπεράσματα της εργασίας του (υπερ)εκτιμά ότι ο διπλασιασμός της συγκέντρωσης του διοξειδίου του άνθρακα στην ατμόσφαιρα θα προκαλέσει μια αύξηση στην μέση θερμοκρασία της γήινης επιφάνειας κατά 5 έως 6 ^oC. Επιπλέον, από τους πίνακες που παραθέτει φαίνεται μια λογαριθμική σχέση μεταξύ της αύξησης θερμοκρασίας συναρτήσει της συγκέντρωσης του διοξειδίου του άνθρακα.

Στη συνέχεια θα αναζητήσουμε μια εξίσωση που να συνδέει απευθείας την συγκέντρωση του διοξειδίου του άνθρακα με την μεταβολή της μέσης θερμοκρασίας στην επιφάνεια της Γης.

 Το μέγεθος RF

Oι κλιματολόγοι αναφέρονται συνήθως σε μια εξίσωση που συνδέει την μεταβολή της θερμοκρασίας με το μέγεθος RF (radiative forcing). Ο εξαναγκασμός (θερμικής) ακτινοβολίας RF μετριέται σε W/m² και εκφράζει την μεταβολή στο ενεργειακό ισοζύγιο του πλανήτη εξαιτίας της μεταβολής κάποιας παραμέτρου που επηρεάζει το κλίμα.

H ισορροπία της θερμικής ακτινοβολίας της Γης επιτυγχάνεται όταν στην κορυφή της ατμόσφαιρας η εισερχόμενη ηλιακή ακτινοβολία ισούται με την εξερχόμενη ακτινοβολία. Η εξερχόμενη ακτινοβολία, αν εξαιρέσουμε την ανακλώμενη ηλιακή στην κορυφή της ατμόσφαιρας (albedo), είναι η υπέρυθρη ακτινοβολία (μεγάλα μήκη κύματος), που εκπέμπει το σύστημα της (γήινης) επιφάνειας+ατμόσφαιρα.

Ας υποθέσουμε ότι ένας σταθερός θετικός εξαναγκασμός (θερμικής) ακτινοβολίας RF εφαρμόζεται συνεχώς στο σύστημα (γήινης) επιφάνειας-ατμόσφαιρας. Μετά από ένα αρκετά μεγάλο χρονικό διάστημα, η θερμοκρασία του συστήματος θα αυξηθεί έως ότου η αύξηση της ροής της εξερχόμενης ακτινοβολίας στην κορυφή της ατμόσφαιρας γίνει ίση με τον RF, αποκαθιστώντας τη θερμική ισορροπία στον πλανήτη. Eπομένως η μεταβολή της ροής της εξερχόμενης ακτινοβολίας στην κορυφή της ατμόσφαιρας ισούται με τον εξαναγκασμό (θερμικής) ακτινοβολίας RF. Αν το RF είναι αρκετά μικρό, τότε η μεταβολή της παγκόσμιας μέσης επιφανειακής θερμοκρασίας, ΔT_S, αναμένεται επίσης να είναι σχετικά μικρή. Σ' αυτή την περίπτωση ισχύει η σχέση: ΔΤ_s=RF/λ, όπου λ είναι μια κρίσιμη παράμετρος που εκφράζει την μέση μεταβολή της εξερχόμενης ακτινοβολίας στην κορυφή της ατμόσφαιρας που οφείλεται στην μεταβολή κατά μια μονάδα της μέσης επιφανειακής θερμοκρασίας Τ_S. Η εξίσωση ΔΤ_s=RF/λ εκφράζει την κλιματική ευαισθησία (climate sensitivity), και βέβαια δεν έχει καμία σχέση με τα ανθρώπινα συναισθήματα όσον αφορά την κλιματική αλλαγή. Μας δίνει την μεταβολή της μέσης επιφανειακής θερμοκρασίας, εξαιτίας της μεταβολής ενός κλιματικού παράγοντα, όπως η μεταβολή της συγκέντρωσης των αερίων θερμοκηπίου.

άσκηση: Να αποδειχθεί η εξίσωση RF=λ∙ΔΤ_s χρησιμοποιώντας απλή φυσική. Υπενθυμίζεται ότι η ηλιακή σταθερά Ι_Γ=1361 W/m² είναι η ενέργεια της ηλιακής ακτινοβολίας που προσπίπτει ανά δευτερόλεπτο κάθετα σε μια επιφάνεια ενός τετραγωνικού μέτρου, που βρίσκεται στην µέση απόσταση Γης-Ήλιου), και ότι από αυτή την ακτινοβολία το 30% ανακλάται πίσω στο διάστημα (albedo=>α=0,3). Έτσι, κατά μέσο όρο σε ολόκληρη την υδρόγειο, η εισερχόμενη ηλιακή ακτινοβολία στην κορυφή της ατμόσφαιρας είναι

Ι_εισ=Ι_Γ(1–α)∙πR²/4πR²= Ι_Γ(1–α)/4.

Όταν ο πλανήτης βρίσκεται σε θερμική ισορροπία με μια μέση επιφανειακή θερμοκρασία Τ_S, τότε η εισερχόμενη ακτινοβολία στην κορυφή της ατμόσφαιρας θα ισούται με την εξερχόμενη υπέρυθρη ακτινοβολία που εκπέμπει το σύστημα γης-ατμόσφαιρας: Ιεισ=Ιεξ. Σύμφωναν με το νόμο Stefan-Boltzmann και το γεγονό ότι το σύστημα Γη-ατμόσφαιρα δεν είναι τέλειο μέλαν σώμα, θα ισχύει: Ι_εξ=ε∙σ∙Τ_S⁴, όπου Τ_S η μέση θερμοκρασία της Γης και ε<1 o συντελεστής εκπομπής ακτινοβολίας (στο εύρος της υπέρυθρης) του συστήματος, όπου σ=5,67∙10^-8 W∙m^-2K^-4. Εφόσον Ι_εισ=Ι_εξ, προκύπτει ότι:

ε∙σ∙Τ_S⁴=Ι_Γ(1–α)/4 (1)

Αν η θερμοκρασία μεταβληθεί κατά ΔΤ_S, εξαιτίας π.χ. της αύξησης της συγκέντρωσης ενός αερίου θερμοκηπίου στην ατμόσφαιρα, τότε η μεταβολή της εκπεμπόμενης θερμικής ακτινοβολίας από την Γη μετά την αποκατάσταση της νέας θερμικής ισορροπίας θα ισούται με τον εξαναγκασμό (θερμικής) ακτινοβολίας, δηλαδή:
RF=ΔΙ_εξ=I_εξ,τελ–I_εξ,αρχ=ε∙σ∙(T_S+ΔT_S)⁴–ε∙σ∙Τ_S⁴=ε∙σ∙Τ_S⁴(1+ΔΤ_S/Τ_S)⁴–ε∙σ∙Τ_S⁴ ή RF≈4ε∙σ∙Τ_S⁴ΔT_S/Τ_S, δεδομένου ότι (1+ΔΤ_S/Τ_S)⁴≈1+4ΔT_S/Τ_S. Xρησιμοποιώντας την εξ (1) παίρνουμε: $ RF=\lambda \Delta T_{S} \approx \frac{I_{\Gamma}(1-a)}{T_{S}} \Delta T_{S}$, απ' όπου για Τ_S≈288K (ή 15^oC) προκύπτει ότι ΔT_S≈0,3RF (RF σε W/m² και ΔΤ_S σε Κelvin).

Μια αξιόπιστη εκτίμηση της παραμέτρου λ αποτελεί ένα από τα δυσκολότερα επιστημονικά προβλήματα στην σημερινή εποχή. Για παράδειγμα οι τιμές του λ που υπολογίστηκαν ανεξάρτητα από τα δύο πρώιμα κλιματικά μοντέλα (GFDL και NASA/GISS) διέφεραν μεταξύ τους σημαντικά (κατά έναν παράγοντα περίπου δύο). Αλλά μια παρόμοια μεγάλη διαφορά εξακολουθεί να παραμένει μεταξύ των ευαισθησιών που υπολογίζουν και πιο πρόσφατα κλιματικά μοντέλα και γι αυτό επείγει η περαιτέρω βελτίωσή τους.

Διπλασιάζοντας την συγκέντρωση διοξειδίου του άνθρακα

Αν βρούμε μια σχέση που να συνδέει τον εξαναγκασμό (θερμικής) ακτινοβολίας RF που οφείλεται στην αύξηση της συγκέντρωσης του διοξειδίου του άνθρακα στην ατμόσφαιρα, τότε διαμέσου της ΔΤ_s=RF/λ, προκύπτει αμέσως η απευθείας σύνδεση της συγκέντρωσης CO₂ με την μεταβολή της μέσης θερμοκρασίας της Γης. Αλλά αυτό είναι μάλλον δύσκολο να προκύψει αναλυτικά(;).

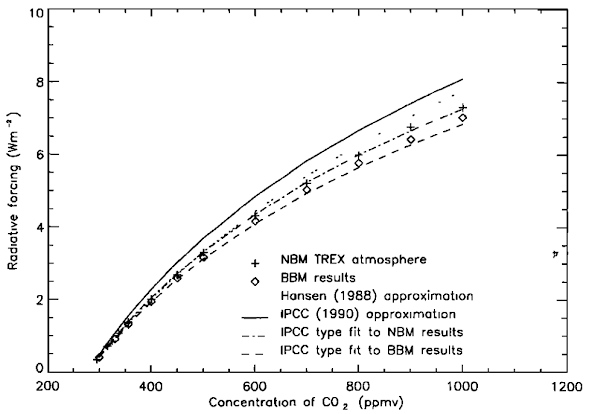
Όπως προαναφέρθηκε, ο Arrhenius ήταν ο πρώτος που υποψιάστηκε ότι μια λογαριθμική σχέση συνδέει τα μεγέθη ΔΤ_s και συγκέντρωση [CO₂], επομένως και τα μεγέθη RF - [CO₂]. Κι έτσι είναι, αφού οι πιο πρόσφατες εκτιμήσεις [Gunnar Myhre et al] μας δίνουν την σχέση: RF_CO2=5,35∙ln(C/C₀), όπου C η συγκέντρωση του CO₂ και C₀≈278ppm (η συγκέντρωση του CO₂ στο ξεκίνημα της βιομηχανικής επανάστασης). Αντικαθιστώντας στην προσεγγιστική εξίσωση ΔT_S≈0,3RF_CO2 που προσδιορίσαμε παραπάνω, παίρνουμε μια εκτίμηση της μεταβολής της μέσης γήινης θερμοκρασίας συναρτήσει της συγκέντρωσης του διοξειδίου του άνθρακα:

ΔT_S≈1,62∙ln(C/278)

Παρατηρούμε ότι αν η συγκέντρωση του διοξειδίου του άνθρακα διπλασιαστεί, τότε προκύπτει μια αύξηση κατά 1,2 Κ (ή ^οC) της μέσης θερμοκρασίας του πλανήτη. Το αποτέλεσμα αυτό είναι ένα κάτω όριο στην κλιματική ευαισθησία - σε σχέση με την συγκέντρωση του διοξειδίου του άνθρακα - που προσδιορίζουν τα περίπλοκα κλιματικά μοντέλα. Για παράδειγμα στο μοντέλο GFDL ο διπλασιασμός της συγκέντρωσης του CO₂ έδινε μια αύξηση θερμοκρασία κατά 2 Κ, ενώ στο μοντέλο NASA/GISS, αύξηση κατά 4 Κ.

 7/1/2022