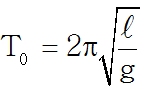Με την εξίσωση που μαθαίνουμε στο σχολείο
Η περίοδος του απλού εκκρεμούς στην πραγματικότητα εξαρτάται από το πλάτος της ταλάντωσης - την αρχική γωνία θο.
Η εξίσωση της περιόδου εξαρτάται από το πλάτος όπως φαίνεται στην παρακάτω εξίσωση
ή σε πιο κλειστή μορφή
Όμως πιο επίσημη έκφραση για την περίοδο του εκκρεμούς είναι η
Όπου το
είναι ένα πλήρες ελλειπτικό ολοκλήρωμα πρώτου είδους.
Οι τιμές του ολοκληρώματος $K(k^{2})$ υπολογίζονται εύκολα. Έστω ότι θέλουμε να υπολογίσουμε την τιμή $Κ(0.5)$, που αντιστοιχεί σε ταλάντωση του εκκρεμούς για αρχική γωνία $θ_{0}=90^{o}$. Αφού μεταβούμε στη διεύθυνση http://www.wolframalpha.com/ γράφουμε στη γραμμή εντολών απλά $Κ(0.5)$ και παίρνουμε την τιμή 1.85407…και η ακριβής περίοδος του εκκρεμούς θα είναι
$$Τ =2Τ_{0}/\pi = T_{0} \cdot 1,1803376…$$ Αλλά ακόμη κι αν διαθέτουμε μόνο έναν απλό υπολογιστή τσέπης (!!) μπορούμε να κάνουμε τον υπολογισμό του παραπάνω ολοκληρώματος και της περιόδου του εκκρεμούς ως εξής:
βήμα 1ο : Βρίσκουμε τον αριθμό:
βήμα 2ο : Υπολογίζουμε τον αριθμητικό και τον γεωμετρικό μέσο των αριθμών 1 και a0 . Έτσι προκύπτουν οι αριθμοί:
βήμα 3ο : Υπολογίζουμε πάλι τον αριθμητικό και γεωμετρικό μέσο των αριθμών a1 και b1 οπότε προκύπτουν δυο νέοι αριθμοί
βήμα 4ο : Κάνουμε το ίδιο για τους a2 και b2 , οπότε
Οι τιμές του ολοκληρώματος $K(k^{2})$ υπολογίζονται εύκολα. Έστω ότι θέλουμε να υπολογίσουμε την τιμή $Κ(0.5)$, που αντιστοιχεί σε ταλάντωση του εκκρεμούς για αρχική γωνία $θ_{0}=90^{o}$. Αφού μεταβούμε στη διεύθυνση http://www.wolframalpha.com/ γράφουμε στη γραμμή εντολών απλά $Κ(0.5)$ και παίρνουμε την τιμή 1.85407…και η ακριβής περίοδος του εκκρεμούς θα είναι
$$Τ =2Τ_{0}/\pi = T_{0} \cdot 1,1803376…$$ Αλλά ακόμη κι αν διαθέτουμε μόνο έναν απλό υπολογιστή τσέπης (!!) μπορούμε να κάνουμε τον υπολογισμό του παραπάνω ολοκληρώματος και της περιόδου του εκκρεμούς ως εξής:
βήμα 1ο : Βρίσκουμε τον αριθμό:
Παρατηρούμε ότι οι αριθμοί συμπίπτουν και δεν έχει νόημα να επαναλάβουμε την διαδικασία (εφόσον θέλουμε ακρίβεια 5 δεκαδικών ψηφίων) διότι θα προκύπτει ο ίδιος αριθμός.
Τελευταίο βήμα: Αντιστρέφουμε την οριακή τιμή που υπολογίστηκε παίρνοντας την τιμή 1/0,847213=1,1804
Που δεν είναι τίποτε άλλο από το πηλίκο $T/T_{0}$ !!
Η τελευταία κομψή μέθοδος οφείλεται σε μια όμορφη ιδιότητα των ελλειπτικών ολοκληρωμάτων που πρώτος απέδειξε ο μεγάλος μαθηματικός Κ. F. Gauss: https://www.scribd.com/fullscreen/44424010?access_key=key-2fx1f25210lhxvz5j06a
Τελευταίο βήμα: Αντιστρέφουμε την οριακή τιμή που υπολογίστηκε παίρνοντας την τιμή 1/0,847213=1,1804
Που δεν είναι τίποτε άλλο από το πηλίκο $T/T_{0}$ !!
Η τελευταία κομψή μέθοδος οφείλεται σε μια όμορφη ιδιότητα των ελλειπτικών ολοκληρωμάτων που πρώτος απέδειξε ο μεγάλος μαθηματικός Κ. F. Gauss: https://www.scribd.com/fullscreen/44424010?access_key=key-2fx1f25210lhxvz5j06a